Preprint
Article
Mixing renewable energy with pumped hydropower storage: Design optimization under uncertainty and other challenges
Altmetrics
Downloads
144
Views
45
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
05 July 2023
Posted:
06 July 2023
You are already at the latest version
Alerts
Abstract
Hybrid renewable energy systems (HRES), complemented by pumped hydropower storage (PHS), have become increasingly popular amidst the increase of renewable energy penetration. This con-figuration is even more prosperous in remote regions that are typically not connected to the mainland power grid, where the energy independence challenge intensifies. This research focuses on the design of such systems, from the perspective of establishing an optimal mix of renewable sources that takes advantage of their complementarities and synergies, combined with the versatility of PHS. However, this design is subject to substantial complexities, due to the multiple objectives and constraints to fulfill, on the one hand, and the inherent uncertainties as well, that span over all underlying processes, i.e., external, and internal. In this vein, we utilize a proposed HRES layout for the Aegean Island of Sifnos, Greece, to develop and evaluate a comprehensive simulation-optimization scheme in deterministic and, eventually, stochastic setting, revealing the design problem under the umbrella of uncertainty. In particular, we account for three major uncertain elements, namely the wind velocity (natural process), the energy demand (anthropogenic process), and the wind-to-power conversion (internal process, expressed in terms of a probabilistic power curve). Emphasis is also given to the decision-making procedure, which requires a thorough interpretation of the uncertainty-aware optimization outcomes. Finally, since the proposed PHS uses the sea as the lower reservoir, additional technical challenges are addressed.
Keywords:
Subject: Engineering - Energy and Fuel Technology
1. Introduction
Hybrid renewable energy systems (HRES), which were first introduced in the 1970s, have become an essential part of global energy production, addressing limitations in terms of fuel flexibility, efficiency, reliability, emissions, and economics [1]. They generate electricity from two or more energy sources, while sharing a single connection point, allowing them to switch between energy sources when one is insufficient, thus reducing the inherited unpredictability of renewable energy sources. HRES can also capitalize on existing energy infrastructure and add components to help reduce costs, environmental impacts, and system disruptions [2]. Power can be generated based on the demand at any particular site depending on the availability of resources, thus also significantly reducing grid dependence.
The optimal design of an HRES requires the most fitting, efficient, and reliable mix of energy technologies to meet users’ needs. However, the asynchronous production of the intermittent renewable energy sources, against the constant, yet highly fluctuating energy demand, is a major constraint against their large scale integration in the energy grid [3]. Interestingly, the absence of an integrated large energy storage in the grid may result in a maximum of 80% wind penetration for a 100-kW grid, decreasing dramatically as the size of the electricity grid increases, diminishing to as low as 20% for a 10-MW grid [4].
For this reason, the rapid development of hybrid renewable energy systems has necessitated their coupling with energy storage to balance the supply and demand. Notably, large energy storage systems have proven to mitigate wind power curtailment by 10% [5,6,7,8]. Energy storage techniques are distinguished into four basic categories, according to their applications [9]. Low and medium-power applications (i.e., batteries, hydrogen fuel cells, superconductors) concern isolated areas and are used in emergency terminals or individual electrical systems. On the other hand, network connection with peak leveling and power-quality control applications (i.e., hydraulic systems, accumulators and flow batteries, compressed air) are used in power systems that provide energy for greater regions.
Pumped hydro storage (PHS) is the predominant and most reliable energy storage technology, accounting for more than 95% of global cumulative energy storage capacity [10]. Among its various benefits, Rehman et al. [11] highlighted several issues that PHS systems can address, which emerge from the large integration of wind power into the electricity network, such as: (1) handling changes in network impedances due to wind farm connection to the grid and its effects on the remote control-signals, (2) handling of harmonics created by the addition of wind on the grid and (3) stability problems that may occur due to dynamics behaviors of wind farms connected to the grids. PHS systems are also not significantly influenced by the fluctuation in energy production occurring from the intermittent nature of renewables [12]. In contrast, other well-established storage systems, namely batteries, are prone to self-discharge effects when they remain in a loss power state for long periods of time, thus reducing their service life. Though PHS systems have been perceived as prohibitively costly, many studies have been suggesting their economic feasibility, especially in remote areas and islandic systems [13,14,15,16].
HRES combined with PHS (which is in fact a water-energy system) are mainly applicable in non-interconnected power systems, such as the ones found in islands. These are defined by geographical isolation, which constitutes their underwater interconnection to the main grid economically not viable, low power demand, and high electricity production cost due to the importing of fossil fuels [17]. In particular, Greece could greatly benefit from the aforementioned systems, since it consists of 29 non-interconnected islandic complexes [18] and its renewable energy potential is high due to the favorable weather conditions. Moreover, the islands’ population increase during the summer leads to increased peak power demand, which further intensifies the need for energy independence. Today, only two HRES have been installed in non-interconnected Greek islands (i.e., Ikaria, Tilos), as pilot applications, while there are also few other systems under investigation, mainly in research context (e.g.,[19,20,21,22,23]). However, very few of these studies attempt to handle the major issue of uncertainty within the planning and design of such systems (e.g., [24]).
In general, PHS systems are configured as either open- or closed-loop. The first option involves the construction of an upper reservoir that is connected to a natural water source, which plays the role of a lower reservoir. On the other hand, closed-loop PHS systems refer to equally-sized reservoirs without any external hydrological connections, recycling the same amount of water. When PHS is part of a HRES, the storage capacity of the reservoir system is dictated by the power accounting between the highly fluctuating, and uncertain, as well, energy production by other renewables and the associated demand. Yet, conventional design practices follow much more simplified approaches in the context of PHS sizing. In particular, they aim at ensuring energy independence for a given time until the upper reservoir is fully discharged, during which weather conditions will not be favorable to sufficiently satisfy power demand. However, this assumption is too conservative, since it considers the worst-case scenario where energy is exclusively produced from the PHS system. Hence, it is expected to lead to reservoir oversizing, which in turn may threaten the technoeconomic feasibility of the overall project.
Recently, a HRES combining power production from renewables and energy storage through a PHS utilizing seawater was proposed for the island of Sifnos [17]. Its preliminary design followed the aforementioned conventional approach, resulting in a quite large reservoir capacity, if compared to the project scale. This case will serve as a proof of concept to further expand a recently proposed stochastic simulation-optimization framework to the design of HRES [25].
In this vein, this article aims at addressing a twofold objective. First, we investigate whether a more comprehensive optimization approach, driven by a detailed simulation model that accounts for the actual dynamics of water-energy fluxes, can significantly reduce the investment cost of the already proposed solution, by means of a smaller reservoir. Second, we explore the impacts of three key sources of uncertainty to the design procedure, involving two model inputs (wind velocity, as a physical process, and load demand, as an anthropogenic one), as well as the conversion of wind to electricity generation, through the power curves of the associated wind turbines. A parallel objective, originating from the use of the sea as lower reservoir, is to reveal the multiple technical challenges and resulting uncertainties, due to the use of seawater across multiple components of the PHS (corrosion of piping system, pumps and turbines, and risk of groundwater contamination in case of leakage).
2. Study area and proposed layout
Sifnos is a Greek island located in the Western Aegean Sea, Greece, in the Cycladic complex, with an area of 74 km2 and a permanent population of 2,755 residents, as per the 2021 census conducted by the Hellenic Statistical Authority (ELSTAT). Sifnos attracts an average of 100,000 tourists during the summer months. Its energy needs are mainly covered by a 9.0 MW oil power plant, while renewables have a small share in the island’s energy mix. Specifically, there is a 1.20 MW wind park and two photovoltaic parks of a 0.20 MW cumulative installed power. According to an analysis of the island’s energy profile for 2020, performed by the Hellenic Electricity Distribution Network Operator (HEDNO), the total energy demand was 17.3 GWh, while the hourly peak demand was 5.4 MW, occurring during the summer months.
A recent research study [17] investigated the development of a HRES, in the northern part of the island (Figure 1), and its techno-economic perspectives. In particular, they represented the operation of an indicative layout, with different combinations of solar photovoltaic (PV) and wind turbine systems, combined with a PHS that utilizes seawater. The upper reservoir is sited in a plateau, at an elevation of +320 m. This configuration is ideal, as there are no physical obstacles hindering the power production by the wind turbines and the PV’s. Moreover, the favoring topography (i.e., steep yet constant terrain slope) facilitates the works concerning the conveyance system and the pumping station, thus requiring minimal technical interventions. Lastly, as social acceptance has a pivotal role in the implementation of renewable energy projects [26], we highlight that the siting location is secluded, with the nearest settlement being 4 km away.
Key outcome of the preliminary design analysis was the sizing of the PHS, resulting to a quite large storage capacity of 1,100,000 m3. This capacity ensures energy autonomy for up to consecutive 16 days, starting from a fully charged state and without storing any excess energy during that time span.
Keeping the main layout of the aforementioned proposal, we attempt to revise some design quantities, and particularly the reservoir size, following a more integrated simulation-optimization procedure (section 3). Furthermore, we embed the key sources of uncertainty within the design procedure, which is formalized in stochastic terms (Section 4).
3. HRES simulation and optimization
3.1. Configuration and key assumptions of simulation
This sub-section aims to specify the configuration of the HRES and outline the general assumptions of the underlying simulation model. The overall layout follows the one of [17], which has been further specified, after preliminary analysis. Its components are illustrated in the schematic sketch of Figure 2, while its key characteristics are summarized in Table 1. All essential design properties are specified, except for the reservoir active depth and the number of PV modules, which are considered subject to optimization.
The wind turbines’ tower height determines the wind speed values at the hub, which are logarithmically distributed with respect to elevation from the ground. Thus, two different wind turbines were chosen, in order to minimize wind power curtailing due to cut-offs (either from very small or very large wind values). However, it is expected that the interaction between large and small wind turbines (e.g., due to turbulence effects) will reduce the wind speed at the hub of the latter. The adjusted speed is calculated through the formula [27]:
where V0 is the freestream wind speed at the hub height level, a is an induction factor, k is a decay coefficient, L is the distance between the turbines and DL is large turbine’s blade diameter. The a and k values are set equal to 0.10 and 0.038, respectively, as suggested in [27]. In our case, we consider the use of four wind turbines, i.e., two large of 2.3 MW and two small of 0.9 MW nominal power, respectively, distanced at 400 m. It is important to remark that greater distance might seem ideal, since the wind speed reduction is less, but does not necessarily result in optimal layouts [28].
The wind power production for a given wind speed value is calculated by the analytical formula, introduced by Sakki et al. [29]:
where Pmin is the minimum power produced at cut-in conditions, Pmax is the rated power, Vwind is the actual wind speed, Vmin is the cut-in wind speed, Vmax is the cut-out wind speed and a, and b are shape parameters. The two parameters are calibrated against empirically derived power curve data provided by the manufacturer. For the wind turbine types used in our simulation, we get a=2.25 and b=20. We remark that the aforementioned formula can accurately describe the wind speed-to-power conversion process, as it considers turbine-specific characteristics, unlike the high polynomial order formulas that are commonly used to describe the wind power curve ([30,31,32]).
Table 1.
Wind turbine and solar PV properties.
| Wind turbines | ||
|---|---|---|
| Model | Enercon E-44 | Enercon E-70 E4 |
| Rated power (kW) | 900.0 | 2,300.0 |
| Minimum power (kW) | 4.0 | 2.0 |
| Cut-in wind speed (m/s) | 3.0 | 2.5 |
| Rated wind speed (m/s) | 16.5 | 15.0 |
| Cut-out wind speed (m/s) | 34.0 | 34.0 |
| Tower height (m) | 55.0 | 113.0 |
| Rotor diameter (m) | 44.0 | 71.0 |
| Solar panels | ||
| Surface area (m2) | 1.94 | |
| Nominal power (W) | 340.0 | |
| Efficiency (%) | 17.5 | |
The following assumptions are also made for the PHS system:
- The reservoir has a trapezoidal shape, and thus the storage and area curves are linear functions of elevation;
- The intake is set at elevation of 1.2 m from the upper reservoir’s bottom to ensure sufficient capacity for deposit management;
- The pump’s power capacity is 6.0 MW, and is equal to the maximum potential surplus estimated as the difference between the total capacity of wind turbines (6.4 MW) and the minimum hourly demand (0.4 MW), occurring during winter in the night;
- The turbine’s power capacity is also 6.0 MW, which is slightly larger than the maximum hourly load (5.4 MW) in order to account for uncertainties, as discussed later;
- The total efficiency values of turbines and pumps are considered constant and equal to 0.85 and 0.80, respectively;
- The penstock’s length and diameter are 910 m and 1.0 m, respectively, as specified in our preliminary design analysis.
3.2. Breakdown of simulation model
The simulation model represents the system’s operation in hourly time intervals, model and is explained through a flow chart in Figure 3. At each time step, the power accounting is performed, by contrasting the power production by the two renewables (wind, solar) to the actual demand. If there are energy surpluses (PNet > 0), the PHS is set to its charging phase, thus pumping water from the sea to the upper reservoir, provided that there is sufficient storage capacity (Stotal < Smax). Similarly, if there are energy deficits (PNet < 0), the discharge phase starts and the water is released downstream through the turbine, thus generating electrical energy, provided that there is available water stored in the upper reservoir (Stotal > Vdead). This process is repeated until the final step equals the simulation length, which in our case is 20 years. The entire simulation procedure is formulated in the Rstudio programming environment.
3.3. Setup of optimization problem
The techno-economic optimization is a crucial step within the development of complex systems, as it helps assess their feasibility and viability. This procedure involves systematically examining numerous technical, economic, and financial aspects, which are often conflicting ([33,34]).
As already mentioned in Section 3.1, in our specific case we consider as design variables of the system the active depth of the reservoir and the number of PV modules. The optimization of these variables is formulated as a multi-objective problem, by accounting for different performance criteria that are expressed in financial terms and weighted properly, in order to ensure a well-balanced operation of the hybrid renewable energy system.
Specifically, the overall performance measure seeks for contrasting the revenues from electricity production, with the costs of construction, purchase, installation and maintenance (all expressed in terms of Equivalent Annual Cost, for the full depreciation time of the project, i.e., 20 years). The project implementation costs that were accounted for in the economic evaluation are associated with:
- the civil engineering works (excavations, roadworks, etc.);
- the purchase, installation and maintenance of the electromechanical equipment (wind turbines, PVs, pumps, turbines) and the conveyance system (GRP pipes);
- specific works associated with the reservoir waterproofing;
We remark that the aforementioned cost values in this study are following the typical pricing of respective projects in Greece.
A crucial requirement of electricity production systems is their reliability, which is a probabilistic concept, defined as the frequency of load demand satisfaction. In our approach, we utilize the complementary definition of reliability, i.e., failure probability, which is quantified in economic terms and embedded in the optimization by means of an empirical penalty function. In this respect, the optimization aims at ensuring a financially attractive and technically sound investment.
For the optimization, we utilize the evolutionary annealing-simplex algorithm [35]. EAS is a probabilistic heuristic global optimization technique, combining the robustness of simulated annealing in rough response surface with the efficiency of hill-climbing methods in convex areas.
3.4. Results – Benchmark scenario
The design optimization procedure results in an active depth of the reservoir equal to 2.88 m (total 4.08 m, by adding the freeboard of 1.20 m), and thus a storage capacity of 315,195 m3, and a PV power capacity of 1.09 MW. Furthermore, the key metrics of the optimized benchmark scenario are presented in Table 2. We remark that the proposed solution ensures a quite satisfactory reliability level of approximately 95%, thus the existing oil station will only have a complementary role in the island’s energy mix by operating 5% of the time. We also underline that the small capacity factor of the hydropower station (actual vs potential energy production) does not indicate a low performance. In contrast, it reveals its pivotal supporting role in fulfilling the deficits by the other two renewables, especially during peak energy demand periods. As far as the other renewables’ capacity factors are concerned, they are in line with the climatic regime of the study area.
Interestingly, the optimized reservoir size equals less than a third of the one suggested in [17]. However, the two solutions are not fully comparable since different assumptions were made in the overall modeling approach. This analysis will be used as the benchmark to formulate our stochastic optimization approach.
4. Issues of uncertainty in hybrid renewable energy systems
Uncertainty has been a long-lasting issue in the planning, design, assessment and real-time operation of HRES, deriving from multiple drivers. Sakki et al. [25] discriminated such uncertainties into two main categories i.e., exogenous (external) and endogenous (internal). The former category mainly refers to the inherent uncertainty of the system’s drivers, whereas the latter refers to conversion processes and underlying modeling assumptions. In this vein, our study utilizes the aforementioned stochastic optimization framework and applies it to the case of Sifnos, by embedding three key sources of uncertainty (i.e., wind process, energy demand, wind speed-to-power conversion). These uncertainties are briefly described in the following sub-sections, while the computational implementation is thoroughly explained in section 5.
4.1. Wind process uncertainty
Hydrometeorological processes are considered one of the main exogenous uncertainties of a HRES due to the intermittent nature of renewables. Specifically, these concern wind processes (i.e., wind velocity, wind direction) that involve aeolic systems, hydrological processes (i.e., precipitation, streamflow, etc.) that are associated with hydropower systems of all scales (from large reservoirs to small run-off-river plants), as well as solar-related processes (i.e., solar radiation, cloud cover, etc.) that are associated with photovoltaic energy.
Regarding wind power, which is one of the key components of our uncertainty analysis, the mainstream approach to represent the variability of wind velocity is to generate synthetic data at coarse time scales (e.g., monthly or daily) by applying theoretical distribution functions following the statistical regime of the historical data. However, it is well known that wind speed exhibits significant fluctuations even across very small scales, thus requiring a much finer modeling resolution. Furthermore, simple statistical tools fail to capture a key aspect of all hydrometeorological processes, namely the dependencies in time and space. In this respect, the most appropriate approach for representing the full regime of such processes (including wind) are stochastic models, applied at fine scales (typically hourly).
In this context, several researchers performed comprehensive analyses of hydrometeorological data worldwide and proposed suitable stochastic methods for simulating the input drivers of renewable energy systems. For instance, Palma et al. [36] presented a novel methodology to facilitate the selection of a proper time series generation model for renewable energy sources, providing a set of indicators to verify the selected model’s accuracy. Furthermore, other studies also emphasized another key property of such processes, which is referred to as long-term persistence and is associated with the changing climate [37,38,39].
4.2. Energy demand uncertainty
Energy demand is an even more complex source of exogenous uncertainty, as it does not only depend on physical-climatic processes (mainly temperature), but also on highly unpredictable environmental and socioeconomic factors [40]. Uncertainty in electricity demand, both for simulation and forecasting purposes, is a topic of high interest in literature. For instance, a study conducted by Cabeza et al. [41] showed that past energy projections for the energy demand of OECD countries were either consistently overestimated or underestimated. This phenomenon intensifies even more in the islands due to the intensive seasonal power demand variations. Thus, it is essential to accurately represent energy demand in probabilistic terms while designing a HRES. Warren et al. [42] also highlighted three main constituents of uncertainty in energy demand; (1) inherent randomness in the way electricity is consumed, (2) modeling and estimation errors, and (3) uncertainty in the model inputs. Finally, Islam et al. [43] presented various models for short, medium, and long-term energy demand modeling under uncertainties and metrics to evaluate their accuracy effectively.
4.3. Wind-to-power conversion uncertainty
As the penetration of wind power in energy systems increases, several concerns about the uncertainty in wind power generation are raised. Uncertainty in wind power system operations can be categorized between discrete and continuous disturbances [44]. The discrete disturbances to equipment failure, such as generators and transmission lines, were accurately demonstrated in an analysis performed on wind turbine generators by Rezamand et al. [45]. The results indicated that the reliability of wind turbine generators (WTGs) can decline to as low as 67.9% after seven years of operation. The continuous disturbances, which include parameters of the unit commitment problem that vary smoothly (e.g., electricity demand and wind power production), were described in the previous sub-section.
Another type of uncertainty to be considered, which is also emphasized in our study, involves the wind turbine power curves (WTPCs), which have a pivotal role in the context of wind power simulation and forecasting, wind turbine condition monitoring, and in the estimation of wind energy potential [46]. Given that wind turbines are commercial products, the WTPCs are provided by the manufacturers as a graph or as a set of points with a typical wind speed discretization of 0.5 m/s. Actually, these are theoretical relationships exhibiting a wind turbine's standard and experimental behavior [47]. However, a wind turbine operates in complex and variable conditions, which deviate significantly from the stable experimental conditions under which manufacturers test them. Thus, the herein referred to as “theoretical” WTPCs cannot accurately represent the actual behavior of wind turbines that operate in the field [48]. The deviation of wind turbine on-site behavior from the theoretical power curve is thoroughly analyzed in the work of Antoniou et al. [49], whilst several real-world examples are also presented in [50]. For this reason, an ample of deterministic and probabilistic models were developed to produce WTPCs that resemble actual operating conditions. Recently, the focus has been shifted towards the latter since deterministic models provide fixed relationships between wind speed and power generation, failing to reveal the variating and dynamic power generation process [51]. A novel probabilistic WTPC model worth mentioning is the one developed by Yan et al. [52], which considers various model inputs (pitch angle, wind direction) based on three non-parametric algorithms.
A last major issue of uncertainty involves the operation of wind turbines in the high wind speed region. According to the theoretical model, the turbines are forced to interrupt their operation in the so-called cut-off wind speed of 25 m/s. However, due to the stochastic nature of wind, and the uncertainty of the theoretical WTPCs, it is impossible to model in deterministic terms when the wind turbines will shut down, and their downtime [53]. Thus, to prevent frequent shutdowns and restarts, the soft cut-out strategy is implemented by extending the maximum admissible wind speed up to 30-32 m/s, without an abrupt shutdown, through controlling pitch and generator in order to gradually decrease the energy production [54]. Multiple studies have addressed the optimal control of wind turbines during high wind speeds to minimize the uncertainties derived from the wind. Jelavic et al. [55] produced a soft-cut out strategy worst-case scenario algorithm that does not significantly increase fatigue loads. Astolfi et al. [56] performed a SCADA data analysis, extending the power curve of a wind turbine farm in the high-speed region, and concluded that the simulated energy improvement was 0.62%, which equaled 1.80% of the wind farm’s total production. Lastly, Castellani et al. [54] extracted operational data from a 2.3 MW wind turbine, which was then simulated to work with the soft cut-out strategy, producing 1.02 MW more than its initial operating state.
A final source of uncertainty with respect to actual wind power generation, in contrast to the theoretical behavior of the power curve, is associated with monitoring errors. The output power observations are acquired through Supervisory Control And Data Acquisition (SCADA) systems. However, such systems often contain abnormal data and outliers, occurring from wind curtailment, maintenance or other uncontrollable factors [57]. Consequently, these data need to be cleared by appropriate classification algorithms in order to eliminate their adverse effects and improve wind power predictability [58].
5. HRES simulation and optimization under uncertainty
5.1. Incorporating uncertainty in the simulation
Following the uncertainty-aware framework by Sakki et al. [25], we run the design optimization problem in a Monte Carlo context. This involves the formulation of a large number of scenarios (in the specific case, one hundred), which allows for providing equally-probable sets of optimized solutions instead of a unique one.
In section 1, we outlined the three key sources of uncertainty that are embedded in the aforementioned Monte Carlo simulation-optimization approach, distinguishing them into two external processes (wind velocity and energy demand) and an internal one (wind power conversion to electricity). The first two sources of uncertainty are integrated in the simulation by means of synthetic time series that are generated through the anySim package [39], which provides a suite of stochastic models for the simulation of both stationary and cyclostationary processes (in univariate or multivariate mode) that may follow a wide spectrum of distributions. This allows for generating synthetic time series with the desired marginal and stochastic properties, as reflected in the associated historical data [59,60,61]. In our work, we utilize this package, which runs in the R programming environment, to generate 100 synthetic time series of hourly wind velocity and hourly energy demand (one for each scenario), for a 20-year horizon, which is the typical economic lifespan of HRES. Their probabilistic and dependence regime reproduces the one of the corresponding historical data, the length of which (ten years) is rather small for a proper representation of their actual variability, and thus uncertainty.
Regarding the uncertainty in wind velocity to power conversion, as mentioned in section 4, wind turbines operate in complex and variable conditions, thus the power curves provided by the manufacturers do not accurately represent their on-site behavior. In this vein, we follow a Monte Carlo simulation approach, considering that the shape parameters a and b of the empirical Equation (2) are random variables. Specifically, for both turbines the output power for a given wind velocity value is sampled from a normal distribution with a ~ N(2.25, 0.0225) and b ~ N(20, 0.016). This distribution and the associated parameters (i.e., mean and standard deviation values) were appropriately selected, after some trials, so that the average deviation from the theoretical curve is no greater than 15% (Figure 4). This deviation is within reasonable margins, since Lira et al. [62] stated that power curve uncertainty is approximately 10%.
Furthermore, we also implement the soft cut-out strategy, allowing the wind turbine to operate in the high-wind speed region (Figure 4). Therefore, we consider a linear reduction of the turbine’s power for wind speed values between 25 and 30 m/s. The slope, z, of this linear equation is also represented as a normal process, with z ~ N(150, 225) for the large turbines and z ~ N(45, 100) for the small ones.
5.2. Results of Monte Carlo scenarios
Table 3 summarizes the key statistical characteristics of the basic outputs of the 100 optimization scenarios, which are expressed in terms of mean, standard deviation and three typical quantiles, i.e., 10, 50 and 90%. We remind that the two design variables to optimize were the reservoir active depth and the total power capacity of PVs. The conventional approach of section 3 resulted in the optimized values of 2.88 m and 1.09 MW, respectively. However, under the Monte Carlo framework, the reservoir depth and, consequently, its storage capacity, exhibits significant variability, which is propagated in the key performance metrics of the system (net profit and reliability). In contrast, the variability of PV capacity is negligible. In this context, the range of uncertainty with respect to renewable energy production mainly reflects the stochasticity of the wind process and its conversion through the probabilistic power curves of the two turbines. We remark that while the installed wind power capacity remains constant (i.e., 6.4 MW), the capacity factor of the two machines varies (although not significantly), as result of this stochasticity. On the other hand, since for all scenarios we apply the same set of solar radiation data, the capacity factor of PVs remains constant, and equals 0.21.
5.3. Insight into the trade-off between reservoir size and overall system profit
The analysis of the model outcomes under uncertainty reveals the existence of a trade-off between the key design quantity, i.e., the active depth of the reservoir, which dictates its size, and the overall profit of the water-energy system. Since this trade-off embeds all kinds of uncertainties that are included in the simulation-optimization procedure, its quantification and interpretation presuppose the use of advanced stochastic and statistical tools. This objective is implemented via a two-step approach.
First, we investigate the marginal behavior of the two random variables, by assigning suitable statistical distributions, specifically the normal and the log-normal one, to the reservoir active depth and the mean annual profit, respectively (Figure 5). In this context, we utilize the fitdistrplus R package [63], which provides functions for fitting a wide range of univariate distributions to different types of data (continuous censored or non-censored, and discrete as well), also supporting different parameter estimation procedures. In our case, for both variables, we apply the moment-matching estimation method, which involves finding the values of the model parameters that make the data's sample moments equal to the model's corresponding population moments.
After selecting the marginal distributions for the two variables, we investigate their dependencies, by fitting a Gaussian copula, as shown in Figure 6. Notably, the two variables exhibit a quite strong negative correlation, as indicated by the associated Pearson coefficient (R), which equals -0.75. The copula approach enables the formulation of multivariate non-normal distributions by combining given non-normal marginal models, only with dependence patterns. Gaussian copulas are very flexible and have been broadly used for the modelling of dependent variables of any type ([64,65]), as well as for predictive uncertainty assessment studies.
In our case, the copula-based approach provides further insight into the trade-off between the optimized reservoir depth and the associated profit under uncertainty. In particular, for a given depth, and thus a known reservoir size, which is an engineering decision, we may specify a probabilistic range of the anticipated annual profit of the system. On the contrary, a desirable profit threshold corresponds to a range of potential design options. In this vein, a conservative design approach would favor the implementation of a large reservoir (upper quantile) and vice versa. Conclusively, the copula graph can be utilized as a decision support tool for both engineers and from the perspective of investors and stakeholders.
6. The challenge of seawater
One of the major obstacles for the development of HRES in small, non-interconnected islands, which take advantage of PHS, is the scarcity of water resources, which is a long-lasting issue, especially during summer. A potential solution could be the deployment of PHS systems that utilize the sea as the lower reservoir, as proposed in the case of Sifnos island. The Okinawa Yanbaru Seawater Pumped Storage Power Station [66] was the first experimental pumped-storage facility worldwide that used seawater for energy storage. Its construction lasted from 1987 to 1999, yet it was dismantled in 2016. This is because Okinawa’s projections overestimated the load demand growth, constituting the plant’s operation no longer profitable.
Over the years, there have been several studies suggesting the use of PHS systems that utilize the sea as the lower reservoir in islands, including Hawaii, Ireland and Azores [67,68,69]. In a more recent study, Ali and Jang [70] examined the case of Deokjeok-do, South Korea and found that a HRES coupled with a seawater PHS, apart from providing energy independence, also leads to a cheaper initial investment cost than using batteries as energy storage. However, the inclusion of a seawater pumped storage in the HRES introduces various technical challenges, mainly related to corrosion. This section aims to address the most crucial ones, ensuring the proposed system’s technical feasibility.
6.1. Conveyance system
Corrosion prevention can vary depending on whether the components are subject to high or low flow. This protection categorization was implemented in the Okinawa project [71]. The conveyance system of the latter utilized pipes fabricated of Fiber Reinforced Plastic (FRP) with rubber joint seals, which are resistant to both seawater corrosion and high pressure. Generally, Glass Reinforced Polyester (GRP) is chosen for smaller pipe diameters [72]. GRP is a composite material that consists of a polymer matrix and glass fibers. The former is usually an epoxy, vinyl ester, or polyester thermosetting resin, acting as a binder for the fibers, while the latter adds strength to the composite [73]. Its chemical structure is inert to seawater, and its smooth surface reduces hydraulic losses, exhibiting a quite satisfactory friction factor of 0.030. However, this material’s internal water pressure decreases as the pipe’s diameter increases. Nevertheless, GRP pipes can be combined with steel pipes, if higher pressures are expected [72].
Another important issue regarding the conveyance system is the unwanted accumulation of marine organisms immersed in the sea, which is also referred to as marine fouling [74]. In the past, various methods were used to prevent that phenomenon, such as chlorine production by an electrolysis unit and its disposal in the penstock [75]. However, it was found that such practices not only threatened the surrounding ecosystem, but also deposited byproducts (i.e., manganese) [76]. While less harmful methods that do not produce biocidal intermediates have been investigated, i.e., electrochemical degradation ([77]), natural biocide-based and non-stick coatings ([78,79]), further research is required in order to provide solutions that ensure both the surrounding ecosystems’ sustainability and the projects’ techno-economic feasibility.
6.2. Electromechanical equipment
Electromechanical equipment refers to the turbines and pumps used in the PHS system. In HRES, the selection of pumps is a particularly important procedure, as there is a wide variety available in the market, serving various applications. For a project of this scale, centrifugal pumps are recommended, given that they have been previously used for marine applications [80]. Their basic limitation is associated with the intermittent production of renewables, meaning that when weather conditions are not favorable, it may be impossible to develop sufficient head to fill the reservoir. This issue was addressed by Manfrida and Secchi [80], who suggested a configuration including the installation of pumps in parallel, with different flow rates.
Similar to the corrosion of pipes, the erosion of electromechanical equipment poses another technical challenge. Francis and Hebdon [81] distinguished the several types of corrosion from seawater that can affect stainless steel (SS) electromechanical equipment into the following:
- Crevice corrosion, which is the most ordinary form of corrosion, is initiated by changes in the local chemistry within a crevice. It is usually associated with a stagnant solution in the micro-environments that tend to occur in crevices. In a seawater pumps, crevices can be found where seals and impellers are fastened to the shaft, and flange faces are cast in for pipe-work connections;
- Erosion corrosion can occur from the seawater’s rapid flow rate;
- Cavitation occurs when a fluid’s operational pressure drops below its vapor pressure and causes gas pockets and bubbles to form and collapse. This common phenomenon occurs when a pump operates outside its normal design parameters. The formed bubbles erode the steel;
- Corrosion fatigue derives from the combination of alternating or cycling stresses in a corrosive environment, mainly affecting seawater pump shafts.
In general, alloys of stainless steel (i.e., Chromium, Nickel, Molybdenum) have a high pitting resistance equivalent number (PREN), which indicates its corrosion resistance. According to the Norwegian Standards (NORSOK) a PREN number of 40 provides sufficient corrosion resistance to seawater [82].
6.3. Groundwater degradation due to seawater effects
The last challenge introduced by seawater concerns the possibility of ground contamination by salt water (either by leakage or by wind transport). Specifically, groundwater salinization is a crucial environmental issue, especially in areas with karstified underlying geological formations (this is also one of the major shortcomings of the proposed design for Sifnos). Thus, the waterproofing of the reservoir is considered essential while dealing with seawater. In this context, High-Density Polyethylene Geomembranes (HDPE), which are resistant to chemicals and UV radiation, are a potential solution, combined with a drainage system that detects possible leakages [66]. On the other hand, the construction of an embankment around the reservoir can prevent seawater transport through the wind [72].
7. Conclusions
In the present study, we developed a simulation-optimization procedure for the design of HRES in a stochastic setting and assessed it within the preliminary analysis of a proposed scheme for a non-interconnected Aegean Island (Sifnos). The HRES model was based on an hourly time scale simulation approach, accounting for a detailed representation of all important meteorological-energy fluxes. With regards to this, the optimization method opted for a robust and techno-economically sustainable outcome, thus maximizing the project’s mean annual profit until its full depreciation, and simultaneously ensuring high reliability in load demand satisfaction.
The design procedure was formalized by means of one hundred Monte Carlo scenarios, in which we considered three key sources of uncertainty, involving a physical process (wind velocity), an anthropogenic process (load demand) and an internal process (wind power-to-electricity conversion). The quantification and interpretation of uncertainty was facilitated through typical statistical metrics (e.g., empirically-derived quantiles), as well as more advanced probabilistic-stochastic tools. In this context, we applied a copula-based approach to evaluate the trade-offs between two of the most important aspects of the optimization problem, namely the active depth of the storage component (design variable) and the net annual profit (performance metric). Our analysis indicated that this can also serve as a decision support tool for all associated groups of interest (engineers, investors, stakeholders).
Furthermore, the selection of a seawater PHS introduces several challenges, which we briefly highlighted and addressed through effective technological means. To this day, this option has only been practically tested in very limited cases, yet has the potential for wide applicability in islanding areas that suffer from water scarcity (which is also the case for Sifnos). Our analysis indicated that HRES coupled with seawater PHS can provide techno-economically feasible solutions to the matter of energy independence in isolated and islandic regions, thus contributing to the sustainable development of the associated local communities.
Certainty, the overall design of HRES supported by PHS also comprise several other challenges to address, involving the project siting and the synergies between the systems’ components, thus constituting the underlying multiobjective optimization problem even more complex ([83,84]).
In particular, the generic layout of the system should also be investigated from the environmental perspective, since ecologically sensitive areas require careful planning and thorough assessing of the ecosystem impacts. Thus, a HRES feasibility study must be accompanied by a formalized environmental impact assessment (EIA). EIA includes measures to minimize or offset the impacts of the surrounding and broader ecosystem, deriving from the project’s implementation and operation [85]. Mitigation measures refer to scaling down or even relocating the project to reduce the impacts at the source, whereas offset measures compensate for the negative impacts by providing solutions that counterbalance them [86].
On the other hand, the synergy between water and energy components across a HRES can be even more effective, in order to improve its overall performance. A prime example is the installation of floating photovoltaic modules (FPV) on the reservoir [87,88]. Such a configuration can favor both components, since the water cooling effects of evaporation and wind ventilation increase PV energy yield, while the PV modules’ shading effects concurrently limits the losses due to evaporation [89]. Such a layout could also be investigated for the Sifnos case.
The incorporation of environmental issues within the design optimization procedure, and the interactions between the reservoir and the FPVs introduce additional sources of uncertainty, to be accounted for in a future study. There is also an ample of uncertain variables to be included in a forthcoming analysis with respect to external drivers (e.g., solar radiation, energy market) as well as power delivery (e.g., electricity transmission losses, voltage stability and breakeven grid extension distance) [90]. Nevertheless, this study has set all fundamental elements, in terms of theoretical background and computational tools, to address the design of HRES under uncertainty.
Author Contributions
Conceptualization & methodology, A.Z., G.-K.S, and A.E.; formal analysis, A.Z.; writing—original draft preparation, A.Z. and A.E.; visualization, A.Z., G.-K.S; supervision, A.E.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The hourly time series of wind velocity, solar radiation and power demand that have been used as basis for the generation of synthetic data are available at https://doi.org/10.5281/zenodo.8100255, and they are delivered under the Creative Commons Attribution 4.0 International.
Acknowledgments
A preliminary form of this research has been presented in the 2022 European Geosciences Union General Assembly ([91]), as a follow up of the student work conducted within the Undergraduate Course of the School of Civil Engineering, titled “Integrated Project of Hydraulic Engineering”. The first author (A.Z.) expresses his gratitude to the teaching staff (Demetris Koutsoyiannis and Nikos Mamassis), as well as his colleagues Maria-Eleni Pantazi, Marianna Diamanta, Ifigeneia Koutsouradi and Anna Kontaxopoulou.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bajpai, P.; Dash, V. Hybrid renewable energy systems for power generation in stand-alone applications: A review. Renew. Sustain. Energy Rev. 2012, 16, 2926–2939. [Google Scholar] [CrossRef]
- J. J. Ding and J. S. Buckeridge, “Design Considerations for a Sustainable Hybrid Energy System,” Trans. Inst. Prof. Eng. New Zeal. Electr. Eng. Sect., vol. 27, no. 1, pp. 1–5, Nov. 2000, [Online]. Available: https://search.informit.org/doi/10.3316/informit. 2882.
- Amirante, R.; Cassone, E.; Distaso, E.; Tamburrano, P. Overview on recent developments in energy storage: Mechanical, electrochemical and hydrogen technologies. Energy Convers. Manag. 2017, 132, 372–387. [Google Scholar] [CrossRef]
- T. Jacob, “Pumped storage in Switzerland-an outlook beyond 2000,” The Economist, March 2011.
- European Commission, “European Green Deal: New financing mechanism to boost renewable energy.” https://ec.europa.eu/info/news/european-green-deal-new-financing-mechanism-boost-renewable-energy-2020-sep-17_en (accessed Feb. 17, 2023).
- McDowall, J. Integrating energy storage with wind power in weak electricity grids. J. Power Sources 2006, 162, 959–964. [Google Scholar] [CrossRef]
- Bueno, C.; Carta, J. Wind powered pumped hydro storage systems, a means of increasing the penetration of renewable energy in the Canary Islands. Renew. Sustain. Energy Rev. 2006, 10, 312–340. [Google Scholar] [CrossRef]
- Kaldellis, J.K.; Zafirakis, D.; Kavadias, K. Techno-economic comparison of energy storage systems for island autonomous electrical networks. Renew. Sustain. Energy Rev. 2009, 13, 378–392. [Google Scholar] [CrossRef]
- Ibrahim, H.; Ilinca, A.; Perron, J. Energy storage systems—Characteristics and comparisons. Renew. Sustain. Energy Rev. 2008, 12, 1221–1250. [Google Scholar] [CrossRef]
- Dianellou, A.; Christakopoulos, T.; Caralis, G.; Kotroni, V.; Lagouvardos, K.; Zervos, A. Is the Large-Scale Development of Wind-PV with Hydro-Pumped Storage Economically Feasible in Greece? Appl. Sci. 2021, 11, 2368. [Google Scholar] [CrossRef]
- Rehman, S.; Al-Hadhrami, L.M.; Alam, M.M. Pumped hydro energy storage system: A technological review. Renew. Sustain. Energy Rev. 2015, 44, 586–598. [Google Scholar] [CrossRef]
- Li, R.; Wu, B.; Li, X.; Zhou, F.; Li, Y. Design of wind-solar and pumped-storage hybrid power supply system. 2010 3rd International Conference on Computer Science and Information Technology 2010, 5, 402–405. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L. Feasibility study and economic analysis of pumped hydro storage and battery storage for a renewable energy powered island. Energy Convers. Manag. 2014, 79, 387–397. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L.; Peng, J. Technical feasibility study on a standalone hybrid solar-wind system with pumped hydro storage for a remote island in Hong Kong. Renew. Energy 2014, 69, 7–15. [Google Scholar] [CrossRef]
- Al-Addous, M.; Al Hmidan, S.; Jaradat, M.; Alasis, E.; Barbana, N. Potential and Feasibility Study of Hybrid Wind–Hydroelectric Power System with Water-Pumping Storage: Jordan as a Case Study. Appl. Sci. 2020, 10, 3332. [Google Scholar] [CrossRef]
- Makhdoomi, S.; Askarzadeh, A. Techno-enviro-economic feasibility assessment of an off-grid hybrid energy system with/without solar tracker considering pumped hydro storage and battery. IET Renew. Power Gener. 2022, 17, 1194–1211. [Google Scholar] [CrossRef]
- Al Katsaprakakis, D.; Voumvoulakis, M. A hybrid power plant towards 100% energy autonomy for the island of Sifnos, Greece. Perspectives created from energy cooperatives. Energy 2018, 161, 680–698. [Google Scholar] [CrossRef]
- Zafeiratou, E.; Spataru, C. Long Term analysis of submarine transmission grid extensions between the Greek islands and the mainland. 2019 International Conference on Smart Energy Systems and Technologies (SEST) 2019, 1–6. [Google Scholar] [CrossRef]
- P. THEODOROPOULOS, A. ZERVOS, Z. MANTAS, and G. BETZIOS, “Integrated power system of Serifos Island with high RES penetration using pump-storage,” A Chall. Isl. Sustain. Dev., p. 81, 2003.
- Kaldellis, J.; Kavadias, K. Cost–benefit analysis of remote hybrid wind–diesel power stations: Case study Aegean Sea islands. Energy Policy 2007, 35, 1525–1538. [Google Scholar] [CrossRef]
- Kapsali, M.; Anagnostopoulos, J.; Kaldellis, J. Wind powered pumped-hydro storage systems for remote islands: A complete sensitivity analysis based on economic perspectives. Appl. Energy 2012, 99, 430–444. [Google Scholar] [CrossRef]
- Chalakatevaki, M.; Stamou, P.; Karali, S.; Daniil, V.; Dimitriadis, P.; Tzouka, K.; Iliopoulou, T.; Koutsoyiannis, D.; Papanicolaou, P.; Mamassis, N. Creating the electric energy mix in a non-connected island. Energy Procedia 2017, 125, 425–434. [Google Scholar] [CrossRef]
- Skroufouta, S.; Baltas, E. Investigation of hybrid renewable energy system (HRES) for covering energy and water needs on the Island of Karpathos in Aegean Sea. Renew. Energy 2021, 173, 141–150. [Google Scholar] [CrossRef]
- Papoulakos, K.; Pollakis, G.; Moustakis, Y.; Markopoulos, A.; Iliopoulou, T.; Dimitriadis, P.; Koutsoyiannis, D.; Efstratiadis, A. Simulation of water-energy fluxes through small-scale reservoir systems under limited data availability. Energy Procedia 2017, 125, 405–414. [Google Scholar] [CrossRef]
- Sakki, G.; Tsoukalas, I.; Kossieris, P.; Makropoulos, C.; Efstratiadis, A. Stochastic simulation-optimization framework for the design and assessment of renewable energy systems under uncertainty. Renew. Sustain. Energy Rev. 2022, 168. [Google Scholar] [CrossRef]
- Ioannidis, R.; Koutsoyiannis, D. A review of land use, visibility and public perception of renewable energy in the context of landscape impact. Appl. Energy 2020, 276, 115367. [Google Scholar] [CrossRef]
- Vasel-Be-Hagh, A.; Archer, C.L. Wind farm hub height optimization. Appl. Energy 2017, 195, 905–921. [Google Scholar] [CrossRef]
- Hoxha, B.; Shesho, I.K.; Filkoski, R.V. Analysis of Wind Turbine Distances Using a Novel Techno-Spatial Approach in Complex Wind Farm Terrains. Sustainability 2022, 14, 13688. [Google Scholar] [CrossRef]
- Sakki, G.-K.; Tsoukalas, I.; Efstratiadis, A. A reverse engineering approach across small hydropower plants: a hidden treasure of hydrological data? Hydrol. Sci. J. 2021, 67, 94–106. [Google Scholar] [CrossRef]
- Giorsetto, P.; Utsurogi, K.F. Development of a New Procedure for Reliability Modeling of Wind Turbine Generators. IEEE Trans. Power Appar. Syst. 1983, PAS-102, 134–143. [Google Scholar] [CrossRef]
- Thapar, V.; Agnihotri, G.; Sethi, V.K. Critical analysis of methods for mathematical modelling of wind turbines. Renew. Energy 2011, 36, 3166–3177. [Google Scholar] [CrossRef]
- Shokrzadeh, S.; Jozani, M.J.; Bibeau, E. Wind Turbine Power Curve Modeling Using Advanced Parametric and Nonparametric Methods. IEEE Trans. Sustain. Energy 2014, 5, 1262–1269. [Google Scholar] [CrossRef]
- Akram, F.; Asghar, F.; Majeed, M.A.; Amjad, W.; Manzoor, M.O.; Munir, A. Techno-economic optimization analysis of stand-alone renewable energy system for remote areas. Sustain. Energy Technol. Assessments 2020, 38, 100673. [Google Scholar] [CrossRef]
- A. Khatri K C, K. Shah, J. Logeshwaran, and A. Shrestha, “GENETIC ALGORITHM BASED TECHNO-ECONOMIC OPTIMIZATION OF AN ISOLATED HYBRID ENERGY SYSTEM,” vol. 8, pp. 1447–1450, Jan. 2023. [CrossRef]
- A. Efstratiadis and D. Koutsoyiannis, “An evolutionary annealing-simplex algorithm for global optimisation of water resource systems,” 2002, pp. 1423–1428. [CrossRef]
- Palma-Behnke, R.; Vega-Herrera, J.; Valencia, F.; Nunez-Mata, O. Synthetic Time Series Generation Model for Analysis of Power System Operation and Expansion with High Renewable Energy Penetration. J. Mod. Power Syst. Clean Energy 2021, 9, 849–858. [Google Scholar] [CrossRef]
- Tsekouras, G.; Koutsoyiannis, D. Stochastic analysis and simulation of hydrometeorological processes associated with wind and solar energy. Renew. Energy 2014, 63, 624–633. [Google Scholar] [CrossRef]
- Katikas, L.; Dimitriadis, P.; Koutsoyiannis, D.; Kontos, T.; Kyriakidis, P. A stochastic simulation scheme for the long-term persistence, heavy-tailed and double periodic behavior of observational and reanalysis wind time-series. Appl. Energy 2021, 295, 116873. [Google Scholar] [CrossRef]
- Tsoukalas, I.; Kossieris, P.; Makropoulos, C. Simulation of Non-Gaussian Correlated Random Variables, Stochastic Processes and Random Fields: Introducing the anySim R-Package for Environmental Applications and Beyond. Water 2020, 12, 1645. [Google Scholar] [CrossRef]
- Abdel-Aal, R. Univariate modeling and forecasting of monthly energy demand time series using abductive and neural networks. Comput. Ind. Eng. 2008, 54, 903–917. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Palacios, A.; Serrano, S.; Ürge-Vorsatz, D.; Barreneche, C. Comparison of past projections of global and regional primary and final energy consumption with historical data. Renew. Sustain. Energy Rev. 2018, 82, 681–688. [Google Scholar] [CrossRef]
- Warren, K.; Ambrosio, R.; Chen, B.; Fu, Y.H.; Ghosh, S.; Phan, D.; Sinn, M.; Tian, C.H.; Visweswariah, C. Managing uncertainty in electricity generation and demand forecasting. IBM J. Res. Dev. 2016, 60, 8:1–8:13. [Google Scholar] [CrossRef]
- Islam, M.; Che, H.S.; Hasanuzzaman, M.; Rahim, N. Chapter 5 - Energy demand forecasting. In Energy for Sustainable Development; M. D. Hasanuzzaman and N. A. Rahim, Eds., Academic Press; 2019; pp. 105–123. [Google Scholar] [CrossRef]
- Papavasiliou, A.; Oren, S.S.; Aravena, I. Stochastic Modeling of Multi-area Wind Power Production. 2015 48th Hawaii International Conference on System Sciences 2015, 2616–2626. [Google Scholar] [CrossRef]
- Rezamand, M.; Carriveau, R.; Davison, M.; Davis, J.J.; Ting, D.S.-K. Aggregate reliability analysis of wind turbine generators. IET Renew. Power Gener. 2019, 13, 1902–1910. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, Q.; Li, L.; Foley, A.M.; Srinivasan, D. Approaches to wind power curve modeling: A review and discussion. Renew. Sustain. Energy Rev. 2019, 116, 109422. [Google Scholar] [CrossRef]
- Villanueva, D.; Feijóo, A. Comparison of logistic functions for modeling wind turbine power curves. Electr. Power Syst. Res. 2018, 155, 281–288. [Google Scholar] [CrossRef]
- Pagnini, L.C.; Burlando, M.; Repetto, M.P. Experimental power curve of small-size wind turbines in turbulent urban environment. Appl. Energy 2015, 154, 112–121. [Google Scholar] [CrossRef]
- Antoniou, I.; Pedersen, S.M.; Enevoldsen, P.B. Wind Shear and Uncertainties in Power Curve Measurement and Wind Resources. Wind. Eng. 2009, 33, 449–468. [Google Scholar] [CrossRef]
- King, J.; Clifton, A.; Hodge, B.M. Validation of Power Output for the WIND Toolkit, United States. 2014. [Google Scholar] [CrossRef]
- Kusiak, A.; Zheng, H.; Song, Z. On-line monitoring of power curves. Renew. Energy 2009, 34, 1487–1493. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, H.; Liu, Y.; Han, S.; Li, L. Uncertainty estimation for wind energy conversion by probabilistic wind turbine power curve modelling. Appl. Energy 2019, 239, 1356–1370. [Google Scholar] [CrossRef]
- Petrović, V.; Bottasso, C.L. Wind turbine optimal control during storms. J. Physics: Conf. Ser. 2014, 524. [Google Scholar] [CrossRef]
- Castellani, F.; Natili, F.; Astolfi, D.; Cianetti, F. Mechanical behaviour of wind turbines operating above design conditions. Procedia Struct. Integr. 2019, 24, 495–509. [Google Scholar] [CrossRef]
- M. Jelavić, V. Petrović, M. Barišić, and I. Ivanović, “Wind turbine control beyond the cut-out wind speed,” Eur. Wind Energy Conf. Exhib. EWEC 2013, vol. 1, pp. 343–349, Jan. 2013.
- Astolfi, D.; Castellani, F.; Lombardi, A.; Terzi, L. About the Extension of Wind Turbine Power Curve in the High Wind Region. J. Sol. Energy Eng. 2018, 141. [Google Scholar] [CrossRef]
- Luo, Z.; Fang, C.; Liu, C.; Liu, S. Method for Cleaning Abnormal Data of Wind Turbine Power Curve Based on Density Clustering and Boundary Extraction. IEEE Trans. Sustain. Energy 2021, 13, 1147–1159. [Google Scholar] [CrossRef]
- Liang, G.; Su, Y.; Chen, F.; Long, H.; Song, Z.; Gan, Y. Wind Power Curve Data Cleaning by Image Thresholding Based on Class Uncertainty and Shape Dissimilarity. IEEE Trans. Sustain. Energy 2020, 12, 1383–1393. [Google Scholar] [CrossRef]
- Tsoukalas, I.; Papalexiou, S.M.; Efstratiadis, A.; Makropoulos, C. A Cautionary Note on the Reproduction of Dependencies through Linear Stochastic Models with Non-Gaussian White Noise. Water 2018, 10, 771. [Google Scholar] [CrossRef]
- Tsoukalas, I.; Makropoulos, C.; Koutsoyiannis, D. Simulation of Stochastic Processes Exhibiting Any-Range Dependence and Arbitrary Marginal Distributions. Water Resour. Res. 2018, 54, 9484–9513. [Google Scholar] [CrossRef]
- Tsoukalas, I.; Efstratiadis, A.; Makropoulos, C. Building a puzzle to solve a riddle: A multi-scale disaggregation approach for multivariate stochastic processes with any marginal distribution and correlation structure. J. Hydrol. 2019, 575, 354–380. [Google Scholar] [CrossRef]
- A. Lira, P. Rosas, A. Araújo, and N. Castro, “Uncertainties in the estimate of wind energy production,” in Proceedings of the Energy Economics Iberian Conference, Lisbon, Portugal, 2016, pp. 4–5.
- Delignette-Muller, M.L.; Dutang, C. fitdistrplus: AnRPackage for Fitting Distributions. J. Stat. Softw. 2015, 64, 1–34. [Google Scholar] [CrossRef]
- Song, P.X.-K. Multivariate Dispersion Models Generated From Gaussian Copula. Scand. J. Stat. 2000, 27, 305–320. [Google Scholar] [CrossRef]
- Masarotto, G.; Varin, C. Gaussian copula marginal regression. Electron. J. Stat. 2012, 6, 1517–1549. [Google Scholar] [CrossRef]
- Hiratsuka, A.; Arai, T.; Yoshimura, T. Seawater pumped-storage power plant in Okinawa island, Japan. Eng. Geol. 1993, 35, 237–246. [Google Scholar] [CrossRef]
- Akinyele, D.O.; Rayudu, R.K. Review of energy storage technologies for sustainable power networks. Sustain. Energy Technol. Assess. 2014, 8, 74–91. [Google Scholar] [CrossRef]
- Kim, J.; Suharto, Y.; Daim, T.U. Evaluation of Electrical Energy Storage (EES) technologies for renewable energy: A case from the US Pacific Northwest. J. Energy Storage 2017, 11, 25–54. [Google Scholar] [CrossRef]
- Ioakimidis, C.S.; Genikomsakis, K.N. Integration of Seawater Pumped-Storage in the Energy System of the Island of São Miguel (Azores). Sustainability 2018, 10, 3438. [Google Scholar] [CrossRef]
- Ali, S.; Jang, C.-M. Optimum Design of Hybrid Renewable Energy System for Sustainable Energy Supply to a Remote Island. Sustainability 2020, 12, 1280. [Google Scholar] [CrossRef]
- Oshima, K.; Kawai, J.; Otsuka, S.; Wada, T.; Imano, H. Development of Pump-Turbine for Seawater Pumped Storage Power Plant. Hitachi Rev. 1999, 47, 199–202. [Google Scholar] [CrossRef]
- Katsaprakakis, D.A.; Christakis, D.G.; Stefanakis, I.; Spanos, P.; Stefanakis, N. Technical details regarding the design, the construction and the operation of seawater pumped storage systems. Energy 2013, 55, 619–630. [Google Scholar] [CrossRef]
- Jin, N.J.; Hwang, H.G.; Yeon, J.H. Structural analysis and optimum design of GRP pipes based on properties of materials. Constr. Build. Mater. 2013, 38, 316–326. [Google Scholar] [CrossRef]
- Yebra, D.M.; Kiil, S.; Dam-Johansen, K. Antifouling technology—past, present and future steps towards efficient and environmentally friendly antifouling coatings. Prog. Org. Coatings 2004, 50, 75–104. [Google Scholar] [CrossRef]
- Usachev, I.N. Results of 30-year monitoring of the marine concretes and floating structure of the kislogubsk tidal electric power plant in the Far North. Hydrotech. Constr. 1998, 32, 705–712. [Google Scholar] [CrossRef]
- Clark, R.H. Prospects for Fundy tidal power. La Houille Blanche 1997, 83, 79–85. [Google Scholar] [CrossRef]
- Chen, X.; Noy, A. Antifouling strategies for protecting bioelectronic devices. APL Mater. 2021, 9, 020701. [Google Scholar] [CrossRef]
- Abarzua, S.; Jakubowski, S. Biotechnological investigation for the prevention of biofouling. I. Biological and biochemical principles for the prevention of biofouling. Mar. Ecol. Prog. Ser. 1995, 123, 301–312. [Google Scholar] [CrossRef]
- Rittschof, D. Natural product antifoulants: One perspective on the challenges related to coatings development. Biofouling 2000, 15, 119–127. [Google Scholar] [CrossRef] [PubMed]
- Manfrida, G.; Secchi, R. Seawater pumping as an electricity storage solution for photovoltaic energy systems. Energy 2014, 69, 470–484. [Google Scholar] [CrossRef]
- R. Francis and S. Hebdon, “The Selection of Stainless Steels for Seawater Pumps,” Paper 5446; Corrosion 2015; NACE International: Houston, TX, USA, 2015. [Google Scholar]
- N. Standard, “Materials selection,” Nourway, M001 Rev, vol. 4, 2004.
- Das, P.; Das, B.K.; Mustafi, N.N.; Sakir, T. A review on pump-hydro storage for renewable and hybrid energy systems applications. Energy Storage 2020, 3. [Google Scholar] [CrossRef]
- Thirunavukkarasu, M.; Sawle, Y.; Lala, H. A comprehensive review on optimization of hybrid renewable energy systems using various optimization techniques. Renew. Sustain. Energy Rev. 2023, 176. [Google Scholar] [CrossRef]
- Ruiz, R.A.; de Vilder, L.; Prasasti, E.; Aouad, M.; De Luca, A.; Geisseler, B.; Terheiden, K.; Scanu, S.; Miccoli, A.; Roeber, V.; et al. Low-head pumped hydro storage: A review on civil structure designs, legal and environmental aspects to make its realization feasible in seawater. Renew. Sustain. Energy Rev. 2022, 160, 112281. [Google Scholar] [CrossRef]
- EC, “Directive 2014/52/EU of the European Parliament and of the Council of 16 April 2014 amending Directive 2011/92/EU on the assessment of the effects of certain public and private projects on the environment,” Official Journal of the European Union, vol. 50. European Commission Brussels, 2014.
- Dai, J.; Zhang, C.; Lim, H.V.; Ang, K.K.; Qian, X.; Wong, J.L.H.; Tan, S.T.; Wang, C.L. Design and construction of floating modular photovoltaic system for water reservoirs. Energy 2019, 191, 116549. [Google Scholar] [CrossRef]
- Kakoulaki, G.; Sanchez, R.G.; Amillo, A.G.; Szabo, S.; De Felice, M.; Farinosi, F.; De Felice, L.; Bisselink, B.; Seliger, R.; Kougias, I.; et al. Benefits of pairing floating solar photovoltaics with hydropower reservoirs in Europe. Renew. Sustain. Energy Rev. 2023, 171. [Google Scholar] [CrossRef]
- Exley, G.; Armstrong, A.; Page, T.; Jones, I.D. Floating photovoltaics could mitigate climate change impacts on water body temperature and stratification. Sol. Energy 2021, 219, 24–33. [Google Scholar] [CrossRef]
- Faccio, M.; Gamberi, M.; Bortolini, M.; Nedaei, M. State-of-art review of the optimization methods to design the configuration of hybrid renewable energy systems (HRESs). Front. Energy 2018, 12, 591–622. [Google Scholar] [CrossRef]
- A. Zisos et al., “Towards energy autonomy of small Mediterranean islands: Challenges, perspectives and solutions,” in EGU General Assembly Conference Abstracts, in EGU General Assembly Conference Abstracts. May 2022, pp. EGU22-5468. [CrossRef]
Figure 1.
(a) The island of Sifnos and (b) the proposed HRES layout (Source: Google Earth, after processing).
Figure 1.
(a) The island of Sifnos and (b) the proposed HRES layout (Source: Google Earth, after processing).
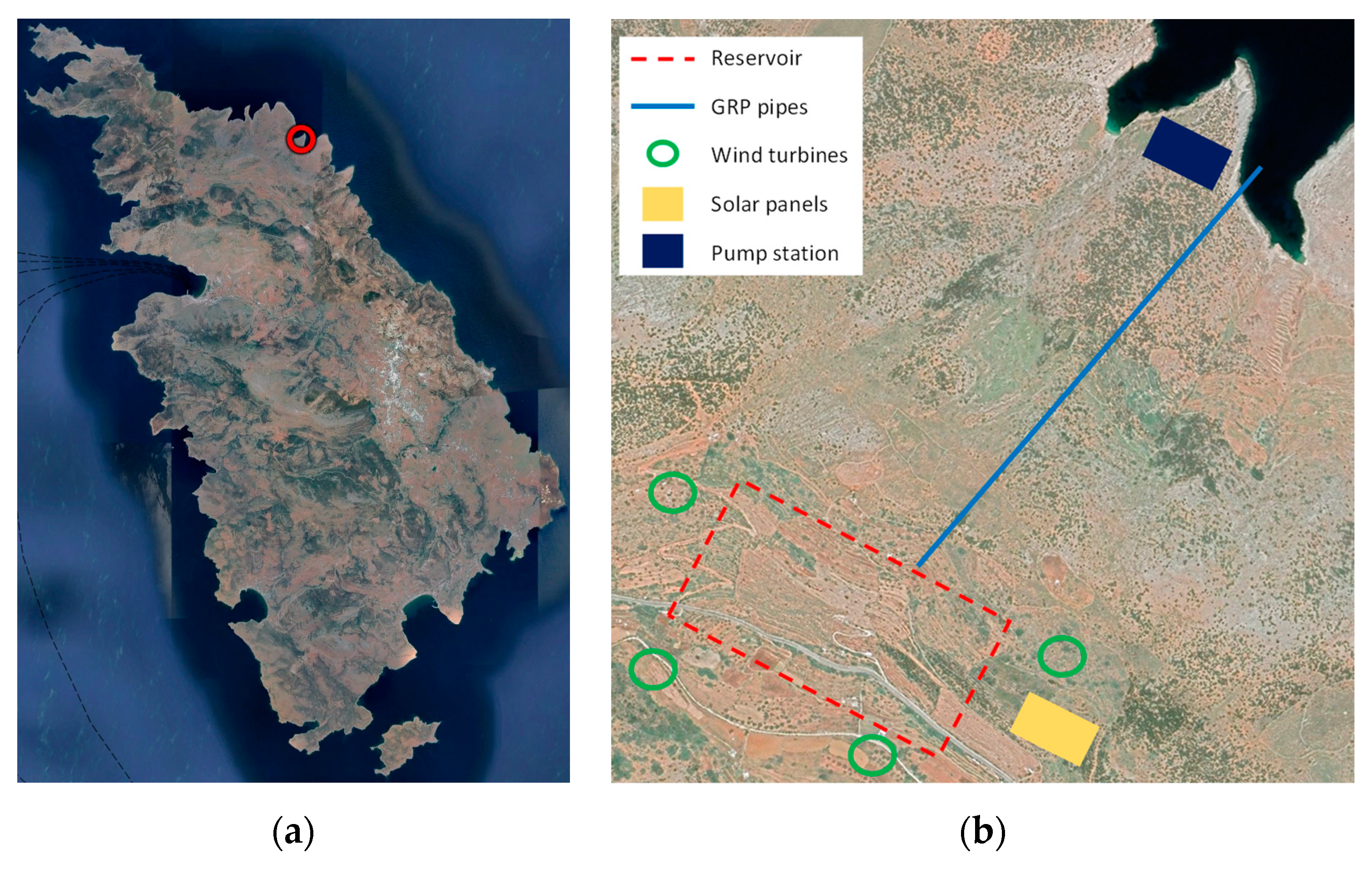
Figure 2.
Configuration of simulation model and associated water-energy fluxes.
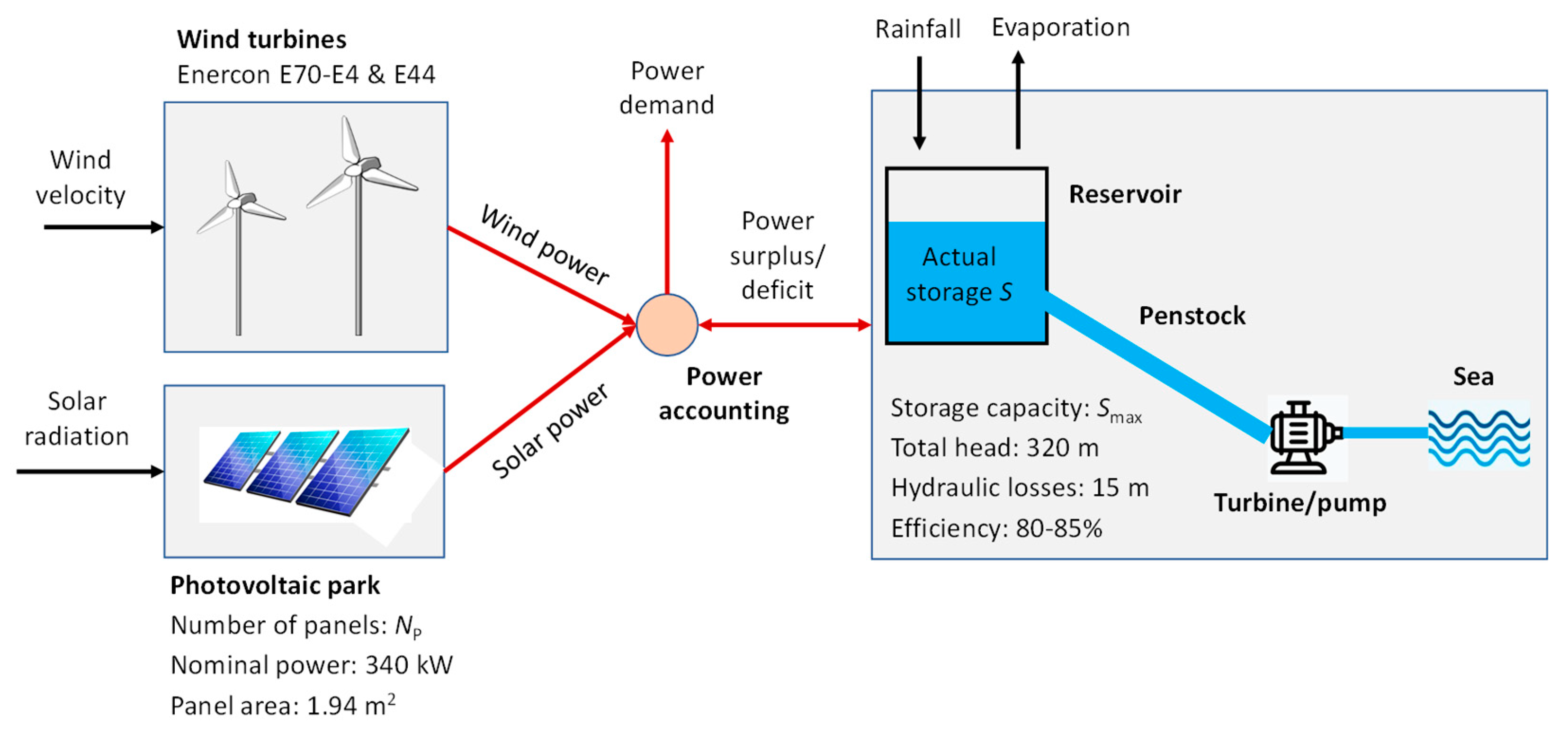
Figure 3.
System operation breakdown.
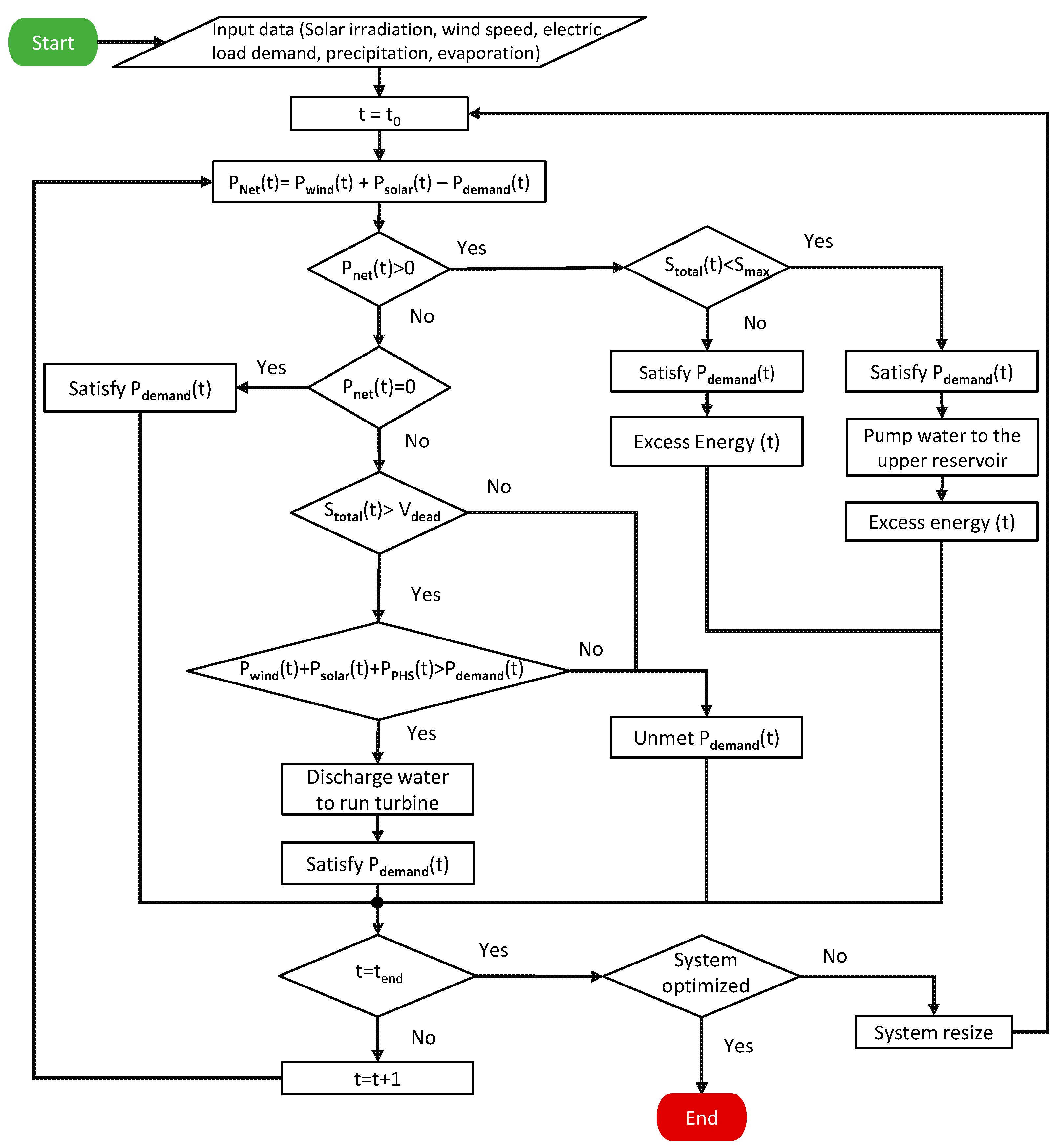
Figure 4.
Example of randomly-generated power curves for (a) the large turbine (E-44) and; (b) the small turbine (E70 E-4).
Figure 4.
Example of randomly-generated power curves for (a) the large turbine (E-44) and; (b) the small turbine (E70 E-4).
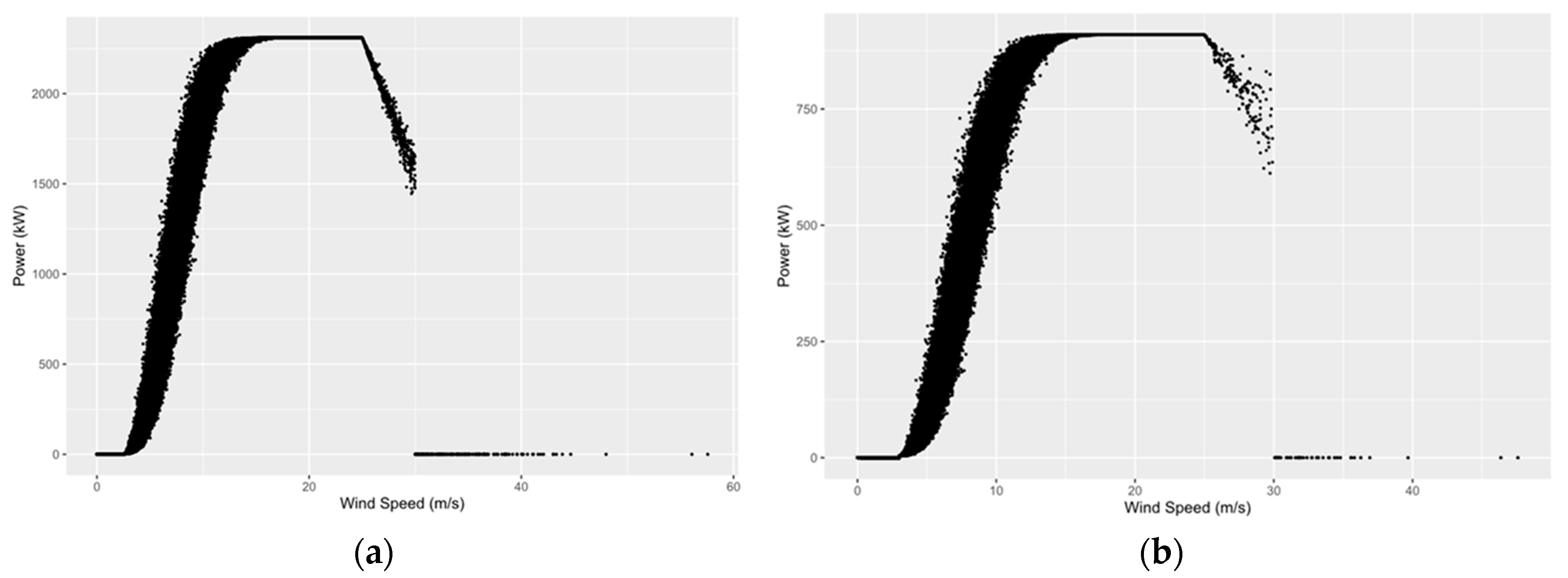
Figure 5.
Fitting of the normal (left) and log normal distributions (right) to the mean annual profit and reservoir active depth, respectively, where: (a) the theoretical density functions and; (b) are the cumulative density functions.
Figure 5.
Fitting of the normal (left) and log normal distributions (right) to the mean annual profit and reservoir active depth, respectively, where: (a) the theoretical density functions and; (b) are the cumulative density functions.
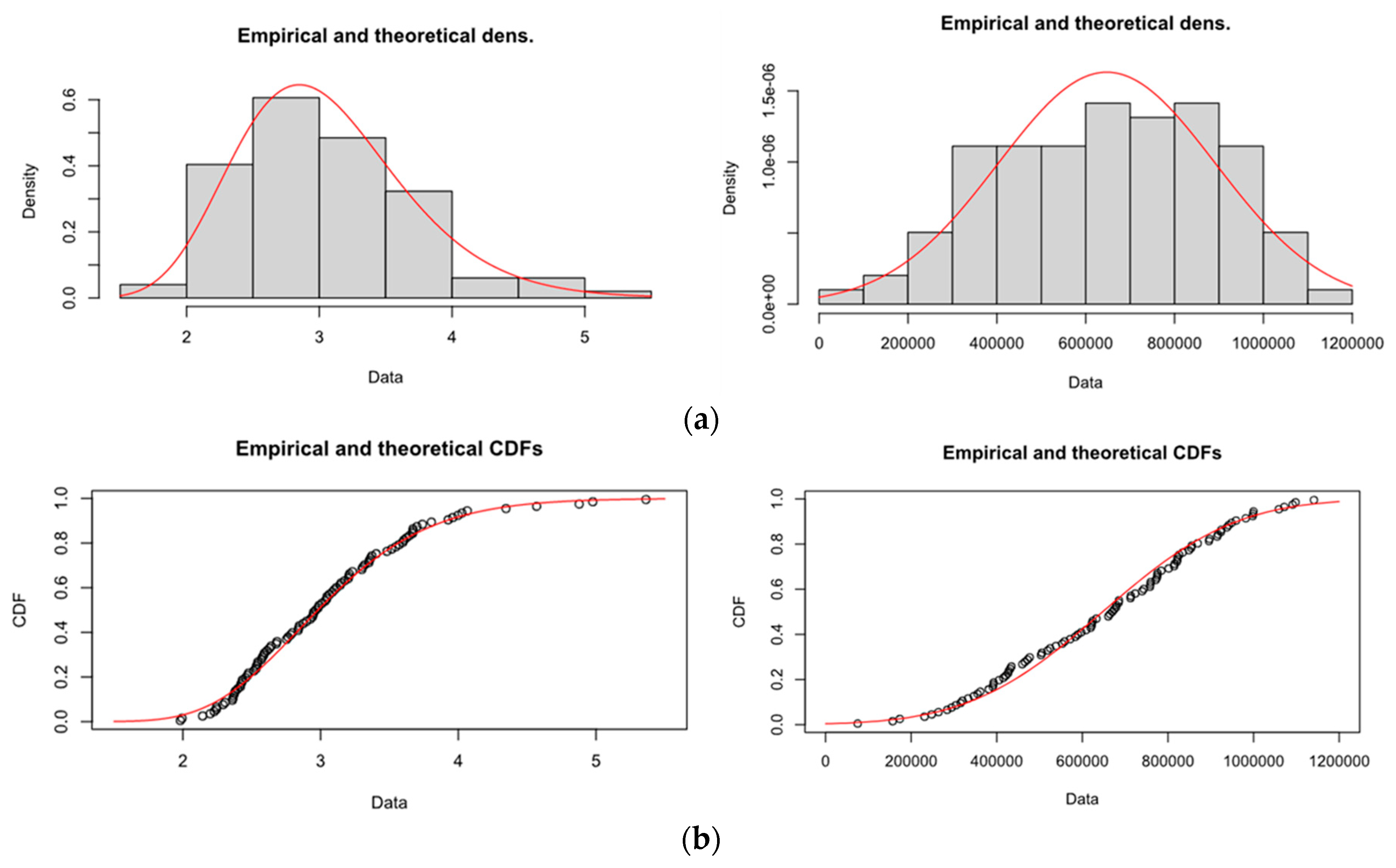
Figure 6.
Fitting of Gaussian copula to mean annual profit and reservoir active depth.
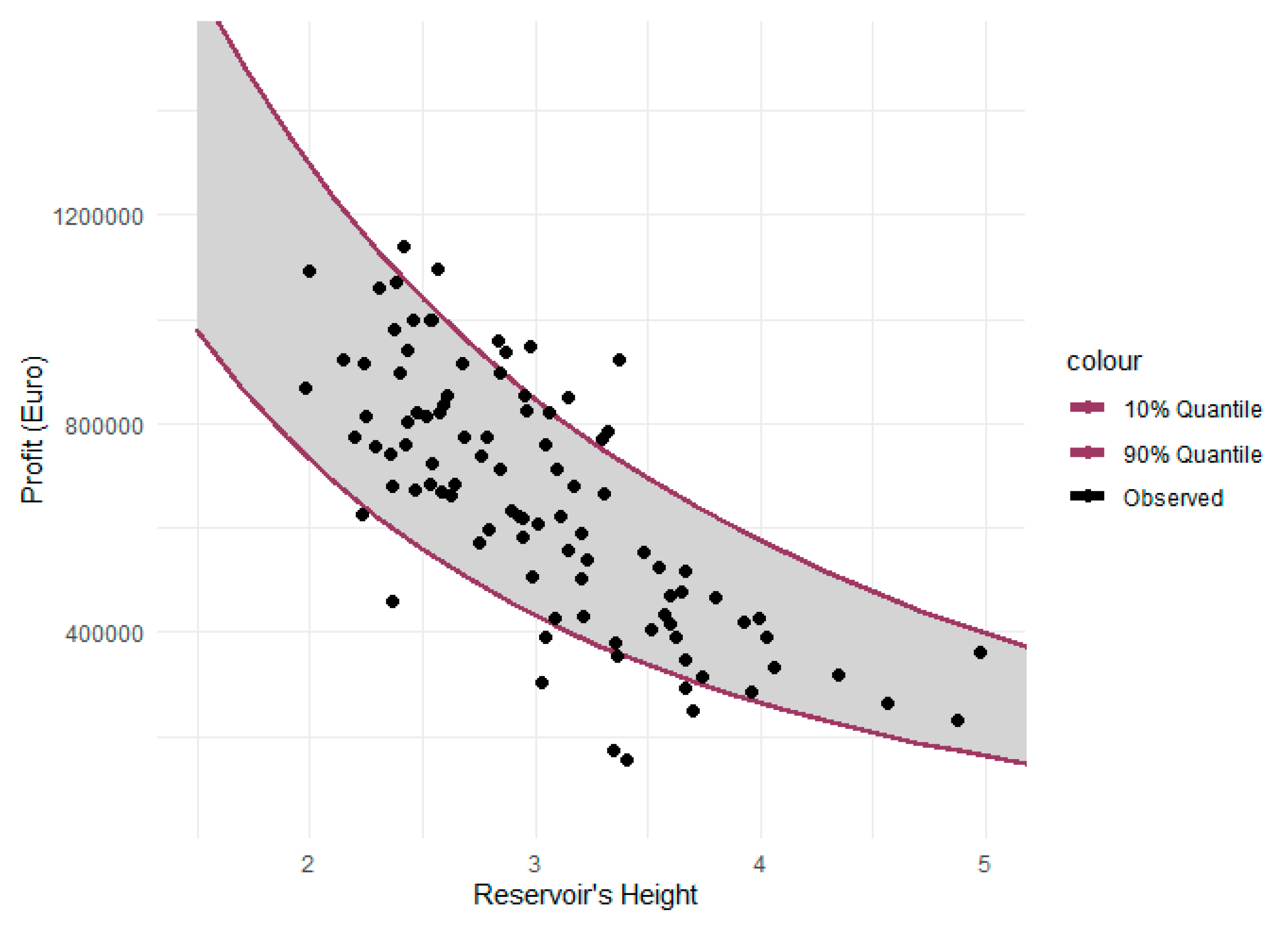
Table 2.
Simulation metrics from the optimized scenario.
| Mean annual production from wind turbines and solar panels (GWh) | 24.98 |
| Mean annual production from PHS (GWh) | 4.69 |
| Reliability (%) | 94.76 |
| Mean annual profit (€) | 789,131 |
| Capacity factor | |
| Photovoltaics | 0.207 |
| Small wind turbines | 0.304 |
| Large wind turbines | 0.424 |
| Hydropower station | 0.108 |
Table 3.
Statistical characteristics of the optimized scenarios (one hundred data sets).
| Mean | Standard deviation | 10% quantile | 50% quantile | 90% quantile | |
|---|---|---|---|---|---|
| Reservoir active depth (m) | 3.07 | 0.76 | 3.96 | 2.98 | 2.36 |
| Reservoir storage capacity (m3) | 329,882 | 53,370 | 400,282 | 323,278 | 274,583 |
| Solar power capacity (MW) | 1.69 | 0.03 | 1.70 | 1.69 | 1.67 |
| Mean annual energy production from wind turbines and solar panels (GWh) | 24.24 | 1.90 | 26.78 | 24.43 | 21.86 |
| Mean annual energy production from PHS (GWh) | 4.93 | 0.19 | 5.16 | 4.95 | 4.69 |
| Reliability (%) | 94.89 | 1.50 | 96.75 | 95.11 | 92.98 |
| Mean annual net profit (€) | 640,234 | 255,062 | 959,029 | 669,924 | 315,269 |
| Capacity factor | |||||
| Small wind turbines | 0.29 | 0.03 | 0.34 | 0.30 | 0.25 |
| Large wind turbines | 0.41 | 0.03 | 0.46 | 0.41 | 0.37 |
| Hydropower station | 0.09 | 0.01 | 0.10 | 0.09 | 0.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







